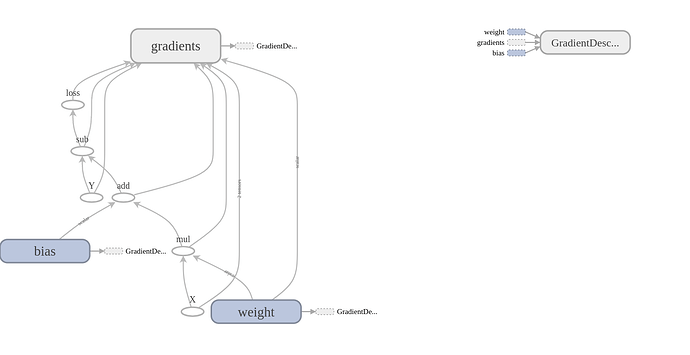
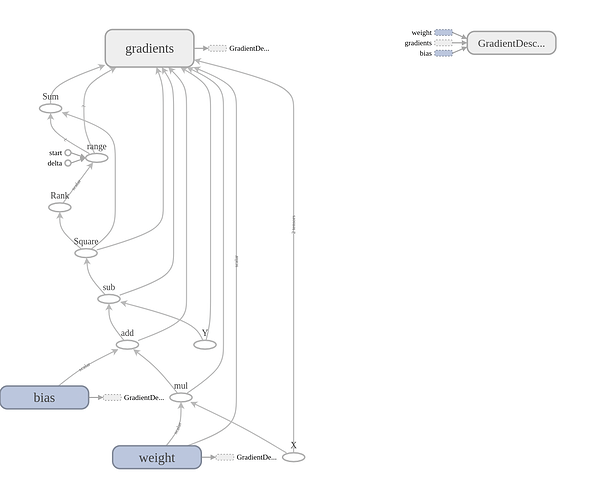
刚开始学习,跟着CS20教程,在第三节用线性回归拟合birth rate和life expectancy的关系时,用给的程序和自己写的程序画出的流图不太一样
第一幅是教程给的程序画的,第二幅是我自己的程序画的,想请教各位大佬,这两种方式在效率或者存储上有区别吗
还有一个困惑,教程给的求loss的方式是loss = tf.square(Y - Y_predicted,name=“loss”),然后运行session,把每对数据得到的loss加到total_loss中,最后求平均,得到的loss是30.04,而我自己的计算方式是loss = tf.reduce_sum(tf.square(linear_model-Y)),然后运行session得到,只有1.53,请问我这种计算方式有什么问题,为什么和所给的loss相差这么大?
caimanong,发表于 2018-6-6 00:14
tf.reduce_mean( tf.square(predict - y) )
reduce_mean不设置其他参数,默认就是整个tensor元素相加取平均,最后返回的是1x1,可以简单理解为一个数。
ZMikkelsen,发表于 2018-6-8 09:57:28
你看一下Y 与 Y_predicted的格式是不是一样,我之前在求均方误差就遇到这样的问题,一个是二维另一个是一维的,计算的话还是有差别的。
Assam,发表于 2018-6-8 21:30:32
我把教程给的代码和我自己的贴上来吧:
教程:
loss = tf.square(Y - Y_predicted, name='loss')
optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(loss)
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(100):
total_loss = 0
for x, y in data:
_, l = sess.run([optimizer, loss], feed_dict={X: x, Y:y})
total_loss += l
avg_loss = total_loss/n_samples
自己:
loss = tf.reduce_sum(tf.square(linear_model-Y))
optimizer = tf.train.GradientDescentOptimizer(0.001)
train = optimizer.minimize(loss)
init = tf.global_variables_initializer()
sess = tf.Session()
sess.run(init)
for i in range(100):
for x, y in data:
sess.run(train, feed_dict={X:x, Y:y})
curr_W,curr_b,curr_loss = sess.run([W,b,loss], {X:x, Y:y})
caimanong(本帖提问者),发表于 2018-6-9 17:18:14
是的,但是我没用tf.reduce_mean,用的是tf.reduce_sum,按理说这种方式是将最终的均方误差相加,得到的loss应该更大才对啊,为什么比教程给的小这么多,画出的拟合曲线,权重偏置都和教程给的结果基本一致,就是计算这个loss差很多。
caimanong(本帖提问者),发表于 2018-6-9 17:39:08
都是一维的向量,其实已经训练出来了,基本能拟合,权重和偏置也都和教程给的基本一致,就是计算这个loss差很多。
caimanong(本帖提问者),发表于 2018-6-9 17:41:02
总的来说,楼主貌似对于这段程序的结构或者对于reduce_sum理解可能有偏差。因为不知道楼主是怎么理解的,我先从基本点说起,如果太过简单或者楼主早就知道了,请见谅。
- 楼主这段程序是一个一个样本进行训练,没有batch,从某种意义上说跟batch_size=1都不一样(模型输入和输出都是零阶张量而不是一阶)。
- reduce_sum是降维求和,在没有其他参数输入的情况下会一路降至零维(输入参数可以选择想要压缩的维度,所以计算图中会有Rank和range节点存在)。由于楼主模型中全是零阶张量,所以reduce_sum等于走过场,这也就回答了楼主的一个问题——这两种方式在效率或者存储上有区别吗——你做了一个没必要的操作,所以有区别但区别又不大,因为反正也是走过场,没啥计算量。关于零阶张量的结论,楼主可以在下面代码的最后输出中看一下第一组样本最后一轮训练loss的输出。
- 我不太确定楼主是怎么比较loss的,如果是拿楼主第一段代码的avg_loss和第二段代码的curr_loss比较,那么这种比较不太合适。从简单统计学角度说,用某一样本的值跟总体平均值比较,会有差别是意料之中的,方差越大,差别就越有可能大。如果楼主对每一样本进行两种损失计算,然后再比较就应该能看到两种计算方法结果完全一样(因为reduce_sum是走过场)。另外,如果楼主画出所有样本的损失值,应该就可以看到损失均值和某些样本的损失应该有较大差别才对。代码如下:
import os
import time
import matplotlib.pyplot as plt
import numpy as np
import tensorflow as tf
tf.logging.set_verbosity(tf.logging.INFO)
import utils
DATA_FILE = 'birth_life_2010.txt'
data, n_samples = utils.read_birth_life_data(DATA_FILE)
X = tf.placeholder(tf.float32, name='X')
Y = tf.placeholder(tf.float32, name='Y')
w1 = tf.get_variable('weights-1', initializer=tf.constant(0.0))
b1 = tf.get_variable('bias-1', initializer=tf.constant(0.0))
Y_1 = w1 * X + b1
loss1 = tf.square(Y - Y_1, name='loss-1')
optimizer1 = tf.train.GradientDescentOptimizer(learning_rate=0.001, name='optimizer1').minimize(loss1)
w2 = tf.get_variable('weights-2', initializer=tf.constant(0.0))
b2 = tf.get_variable('bias-2', initializer=tf.constant(0.0))
Y_2 = w2 * X + b2
loss2 = tf.reduce_sum(tf.square(Y_2 - Y), name='loss-2')
optimizer2 = tf.train.GradientDescentOptimizer(learning_rate=0.001, name='optimizer2').minimize(loss2)
start = time.time()
writer = tf.summary.FileWriter('./linreg', tf.get_default_graph())
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
for i in range(10):
total_loss1 = []
total_loss2 = []
for x, y in data:
_, l1, _, l2 = sess.run([optimizer1, loss1, optimizer2, loss2],
feed_dict={X: x, Y:y})
total_loss1.append(l1)
total_loss2.append(l2)
diff = np.array(total_loss1) - np.array(total_loss2)
print('Differences between loss1 and loss2 in Epoch {0}: {1}'.format(i, diff.sum()))
writer.close()
print(total_loss1[0])
print(total_loss2[0])
plt.plot(total_loss1, label='No reduce')
plt.plot(total_loss2, label='tf.reduce_sum')
plt.legend()
plt.show()
每一轮训练的两种损失计算完全无差别,比如最后一轮训练的输出如下:
Differences between loss1 and loss2 in Epoch 99: 0.0
第一组样本最后一轮训练的两种损失输出如下:
0.93244046
0.93244046
最后一轮训练的所有损失画图如下:
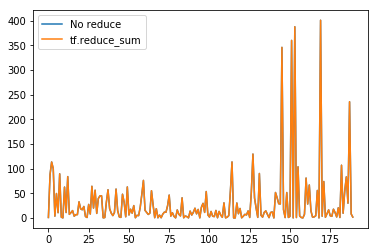
最后补充一下楼主关于效率的问题,如果楼主使用了batch,那么reduce_sum或者reduce_mean是会起作用的,它们是在计算图中求和/求平均,所以可能会比在python代码中求和/求平均有些优势;但更重要的是,使用batch时,很多时候是想要对整个batch的损失进行优化的,这时候需要在计算图中计算损失和/损失平均,必然会选择使用reduce_sum或者reduce_mean(当然也不是100%必然,楼主可能有更好的替代代码)。所以“应该用哪种方式求均方误差”很多时候取决于楼主的模型和训练设计。
yunhai_luo,发表于 2018-6-10 08:07:37
Assam: 大神,冒昧问一句。这里面那个下划线以及op1和op2的作用?
_, l1, _, l2 = sess.run([optimizer1, loss1, optimizer2, loss2],
feed_dict={X: x, Y:y})
yunhai_luo: 下划线跟其他变量一样,也是一个变量,不过约定俗成(没有文档)它代表一个丢弃不用的变量。
optimizer1和optimizer2这里都是优化操作,更新学习后的变量。这个层主估计知道,不知道为何有此一问,能否详解一下想问什么吗?
Assam & yunhai_luo,发表于 2018-6-11 12:07:47
caimanong:
非常感谢您的回答,看了您的解释,终于明白了,我把我自己总结的问题列在这,您看下有没有问题:
1、首先,在这里,确实是一个样本一个样本输入的,在这种情况下,每一次求和的对象只有一个值(0阶张量),所以用tf.reduce_sum()没有意义
2、我搞混了两个概念,即用于训练的loss(用于梯度下降)和最终训练好后计算的loss。因为是一个样本一个样本输入的,所以每一次用于训练的loss只由当前训练的样本计算出来的。教程中是在每一个epoch,都会给出所有样本的平均loss,而这个loss并不用于训练。随着不断训练,该loss不断下降,在最后一个epoch训练结束后,输出的平均loss就可以作为衡量最终模型性能的一个指标。
3、我自己写的有问题,首先最低级的就是x,y是在for循环中定义的,而在求curr_loss却是在循环外,这里没弄明白为什么不会报错,其次,这里的curr_loss是最后一个epoch最后一个样本计算得到的loss(按我那种写法,含义不明,不确定是不是这样),很显然,和最后一个epoch所有样本的平均loss进行比较没有意义,之所以会出现我计算的loss会比教程计算的loss小很多的情况,只是因为最终的模型在最后一个点上拟合较好,但是却不能反映模型的性能,因此我的这种写法有误
4、最后一点,结合其他热心前辈的回答,前面已经说了,一个样本一个样本输入,对于tf.reduce_mean()同样没有意义(两个函数在这种情况下返回的都是原来的值),至于什么时候用tf.reduce_sum()什么时候用tf.reduce_mean(),我还不知道,希望您能传授一点经验。
yunhai_luo:
如果使用tf.reduce_sum(),根据batch_size的大小不同,得到的损失值可能会很大,这样容易导致训练不收敛或误入局部最优解,这个问题有可能通过减小学习速率得到改善,但是使用tf.reduce_mean()不仅可以很好的改善这个问题,而且从某种程度上让你的损失值和训练摆脱对于batch_size的依赖。这是我所知道的两者比较重要的区别,不排除还有其他考量。
caimanong(提问者)& yunhai_luo(最佳答案),发表于:2018-6-18 16:40
我觉得mean和sum效果都一样…
zhanys_7,发表于 2018-7-3 18:29:57
mean和sum其实差不多,,只要你调整一下axis
ViolinSolo,发表于 2018-7-3 20:15:05