文 / Google 机器人团队软件工程师 Xingyou (Richard) Song 和 AI 研究员 Yuxiang Yang
精准度更高的 模拟器引擎 飞速发展,为机器人技术研究人员带来了独特机会,可以生成足够的数据来训练机器人策略,从而完成在现实中的部署。但是,由于模拟域和实际域之间存在细微差异(称为“现实差距”),如何实现训练策略的“从模拟到现实”的迁移仍然是现代机器人技术面临的最大挑战之一。尽管近期的一些学习方法,如模仿学习和离线强化学习等,利用已有的数据来制定策略以解决“现实差距”,但更常见的做法是直接通过改变模拟环境的属性来提供更多数据,这一过程称为 域随机化 (Domain Randomization)。
然而,域随机化会以性能为代价来保持稳定性,因为此过程尝试对所有任务进行优化,寻求一个整体表现良好且稳定的策略,但对改进 特定任务 上的策略并未提供足够的空间。模拟与现实环境之间缺乏通用的最优策略,这是在机器人运动应用中经常会遇到的问题,因为在实际应用中常有多种不同的力在发挥作用,如腿部摩擦力、重力和地形差异的影响等。举例来说,假设机器人的位置和平衡具有相同的初始条件,则最佳策略将由表面类型确定——对于在 模拟 环境中遇到的输入为平坦的平面,机器人加快行进速度,而对于 现实世界 中的崎岖路面,机器人应缓慢而小心行走,以防止跌落。
在《通过进化元学习快速适应行走机器人》 (Rapidly Adaptable Legged Robots via Evolutionary Meta-Learning) 一文中,我们介绍了一种基于 进化策略 (Evolutionary Strategies) 的特殊元学习方法,此方法通常被视为仅在模拟环境下有效,而我们可以按完全无模型的方式高效使用此方法,使得策略能够很好地适应现实环境中的机器人。与之前适应元策略(例如不允许从模拟到现实的应用的标准策略梯度)的方法相比,进化策略 (ES) 可支持机器人快速克服“现实差距”并适应现实环境中的动态变化,而且其中一些变化情况在模拟环境中可能不会出现。这是成功使用 ES 实现机器人适应的第一个实例。

我们的算法可快速调整行走机器人的策略,使其适应动态变化:在此示例中,电池电压从 16.8 伏降至 10 伏,从而可降低电动机功率,同时,我们也在机器人的侧面放置了一块 500 克的物体,以此使其开始转弯而不是直线行走。此策略仅需 50 个回合即可适应(或 150 秒的实际数据)
元学习
此研究属于 元学习 (Meta Learning) 技术范畴,并在行走机器人上得到证明。在较高层次上,元学习可通过将过去的经验与少量来自输入任务的经验相结合,学习快速解决输入任务,而无需从头开始进行再训练。在从模拟到现实的情境下尤其适用,其中 多数 过去的经验都是以较低成本从模拟中获得,而从现实世界中的任务习得的经验虽少,但极为重要。模拟经验使策略具有解决任务分配的一般行为水平,而现实经验使策略能够专门针对当前的具体实际任务进行 微调 。
为训练策略进行元学习,必须要促进策略在模拟期间进行适应。一般来说,可通过应用 模型无关的元学习 (MAML) 来实现这一目标,此模型可使用少量任务特定的数据来搜索可快速适应特定任务的元策略。计算此类元策略的标准方法是使用 策略梯度 方法,此方法旨在提高相同状态下选择相同动作的可能性。为确定选择指定动作的可能性,该策略必须 具有随机性 ,从而使此策略选择的动作具有随机要素。部署此类机器人策略的现实环境也 高度随机 ,因为即使从完全相同的状态和动作序列开始,也会自然产生轻微的运动差异。在随机环境中使用随机策略这一组合会产生两个相互冲突的目标:
- 降低策略的随机性可能至关重要,否则策略动作产生的额外随机性可能会加剧高噪声问题。
- 但是,增加策略的随机性也可能有益于探索,因为策略需要使用随机动作来探测其要适应的环境类型。
这两个相互冲突的目标(之前的 文章 中已有提及)既要降低又要提高策略的随机性,因而可能导致问题变得复杂。
机器人领域中的进化策略
为替代上述方法,我们通过应用 ES-MAML 解决了这些挑战,此算法利用截然不同的范例实现高维优化,即进化策略。ES-MAML 方法仅根据智能体在环境中收集的奖励总和来更新策略。用于优化策略的函数是 黑盒 ,可将策略参数直接映射到此奖励。与策略梯度方法不同,此方法不需要收集状态/动作/奖励元组,也无需估计动作的可能性。因此,可使用 确定性 策略和基于 参数 更改的探索,并能够避免策略和环境随机性之间出现冲突。
在这一范例中,查询通常涉及在模拟器内执行的多个回合,但我们发现 ES 也可以应用于在实际硬件上收集的回合。ES 优化可轻松进行部署,也非常适合用于训练 高效紧凑的策略,这一现象在机器人领域具有深刻意义,因为参数较少的策略能够更容易地部署在实际硬件上,且通常可以提高推理效率并降低功耗。通过学习参数少于 130 个的适应性元策略,我们确认 ES 在训练紧凑型策略方面具备有效性。
ES 优化范例具有非常高的灵活性,可用于优化不可微分的目标,例如我们的机器人示例中的总奖励目标。同时,在具有大量(存在潜在对抗性)的噪声环境下,此优化也能工作。此外,最新形式的 ES 方法(如 引导式 ES)比前代版本具有更高的采样效率。
这样的灵活性对于运动元策略的高效适应至关重要。我们的实验结果表明,使用 ES 进行自适应可通过少量的其他机器人回合来实现。因此,ES 不再只是最先进算法的一种绝佳替代方法,而是代表处理数项高难度 RL 任务的最新技术水平。
模拟环境下的适应
我们首先研究了在模拟环境下使用 ES-MAML 进行训练时出现的适应类型。在模拟环境下测试策略时,我们发现,当动态条件变得过于不稳定时,元策略会迫使机器人跌倒,而适应后的策略则可使机器人恢复稳定并再次行走。此外,当机器人的腿部环境发生更改时,元策略会使机器人的腿无法保持同步,进而导致机器人急转弯,而适应后的策略则会纠正机器人,使其可以再次直行。
在面对困难动态任务时遇到问题的元策略步态。左:元策略导致机器人跌倒;中间:适应后的策略可确保机器人继续正确行走;右:机器人高度的比较测量
机器人的腿部环境更改时的元策略步态。左:元策略使机器人向右侧转弯;中间:适应后的策略可确保机器人继续沿直线行走;右:机器人行走方向的比较测量
现实环境中的适应
尽管 ES-MAML 在模拟环境中表现出色,但将其应用于现实环境中的机器人仍然存在挑战。为了使其有效适应现实世界的噪声环境,同时尽量少使用现实世界的数据,我们引入了 批量爬山算法 ,此算法是在 早期研究成果 之上构建的 ES-MAML 附加组件,用于零阶黑盒优化。与根据确定性目标以迭代方式逐个更新输入的爬山算法不同, 批量爬山算法 对并行查询 批次 进行采样,以此确定下一个输入,从而使其对目标内的大量噪声具有鲁棒性。
我们随后在以下 2 个任务上测试了此方法,而这些任务旨在从机器人的常规环境入手,显著改变动态条件:

在质量电压任务(左)中,我们将 500 克重物放置在机器人的一侧,并将电压从 16.8 伏降至 10.0 伏。在摩擦任务(右)中,我们用网球替代橡胶脚,以大幅减少摩擦并阻碍行走
在质量电压任务中,由于额外增加质量和电压变化,初始元策略使机器人明显向右转向,进而导致机器人的身体和腿部电机失去平衡。但是,在使用我们的方法学习适应 30 个回合之后,机器人能够端正行走姿势,在 50 个回合之后,机器人能够完全保持身体平衡,并且可以行走更长的距离。相比之下, 仅在模拟环境下 通过简单无噪声任务从头开始训练大约需要 90,000 个回合,这表明我们的方法可显著降低昂贵的现实数据的样本复杂性。

质量电压任务中适应阶段的质变
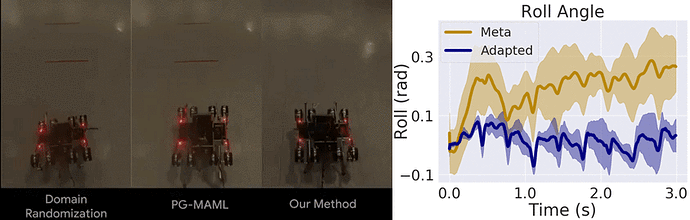
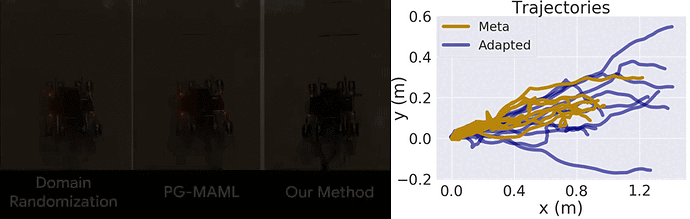
我们仅将我们的方法与域随机化方法以及针对 MAML 的标准策略梯度方法 (PG-MAML) 进行对比,定性地给出了最终策略及来自现实环境机器人的指标,进而展示我们的方法的适应效果。我们发现,域随机化和 PG-MAML 基准的适应效果均不如我们的方法理想。
域随机化和 PG-MAML 之间的比较,以及我们方法的元策略和适应后策略之间的指标差异。上:质量电压任务对比,我们的方法可稳定机器人的侧倾角;下:摩擦任务对比,我们的方法可实现更长的轨迹
未来工作
这项工作为将来的开发提供了几种途径。其中一种选择是对算法进行改进,以减少适应所需的现实环境部署数量。另一个需要改进的领域是将基于模型的强化学习技术用于终身学习系统,在此系统中机器人可以持续收集数据并快速调整其策略,从而学习新技能并在新环境中以最佳的状态运行状态。
致谢
此项研究由 ES-MAML 核心团队完成:Xingyou Song、Yuxiang Yang、Krzysztof Choromanski、Ken Caluwaerts、Wenbo Gao、Chelsea Finn 和 Jie Tan。此外,我们要特别感谢 Vikas Sindhwani 对 ES 方法给予的支持,以及 Daniel Seita 对本文提出的反馈意见。
![]()
原文: Exploring Evolutionary Meta-Learning in Robotics
中文:TensorFlow 公众号